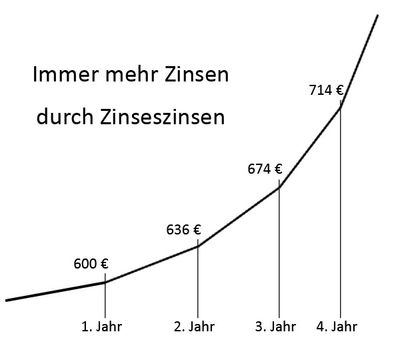
Zinseszinsrechnung
Wenn man z.B. für mehrere Jahre Geld anlegt, hierfür Zinsen erhält, die Zinsen nicht abhebt, dann haben manche Formeln bei der Zinsrechnung einen kleinen Fehler. Denn, nach einer bestimmten Zeit erhält man die Zinsen auf seinem Konto gutgeschrieben. Man müsste also für die Zinsen die man erhalten hat, ebenfalls Zinsen bekommen. Diesen Effekt nennt man Zinseszinsen.
Formelzeichen bei der Berechnung von Zinseszinsen
- Anfangskapital: Formelzeichen K0
- Endkapital: Formelzeichen Kn
- Anzahl der Jahre: Formelzeichen n
- Anzahl der Quartale: Formelzeichen v
- Anzahl der Monate: Formelzeichen m
- Anzahl der Tage: Formelzeichen t
- Zinssatz pro Jahr: Formelzeichen p
- Aufzinsungsfaktor: Formelzeichen q
Ermitteln des Aufzinsungsfaktors (q)
Um die Zinseszinsen zu berechnen, ist vor allem der Aufzinsungsfaktor (q) wichtig. Der Aufzinsungsfaktor bildet den Zinseszins-Effekt ab. Je höher die Anlagedauer, umso höher der Aufzinsungsfaktor. Das Anfangskapital kann mit dem Aufzinsungsfaktor multipliziert werden, um das Endkapital zu ermitteln. Die Formel für den Aufzinsungsfaktor ist:
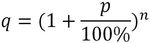
Formeln, um das Endkapital nach n Jahren inkl. Zinseszinsen zu berechnen
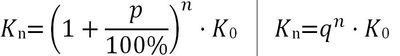
Beispiel:
Anfangskapital (K0): 10000 €
Zinssatz pro Jahr (p): 6%
Anlagedauer (n): 7 Jahre
Gesucht: Endkapital (Kn)
Berechnung: 1 + 6 : 100 = 1,06
1,067 =1,503 (Aufzinsungsfaktor)
1,503 · 10000 € = 15036,30 €
Endkapital bei quartalsweiser, monatlicher oder täglicher Zinszahlung berechnen
Bei vielen Banken erhält man die Zinsen nicht jährlich, sondern quartalsweise, monatlich oder gar täglich. Das würde bedeuten, der Zinseszins-Effekt tritt früher ein als bei einer Zinszahlung nach n Jahren. In solchen Fällen muss der Aufzinsungsfaktor entsprechend den Zinsperioden umgestellt werden. Die Formeln für das Endkapital bei quartalsweiser, monatlicher oder täglicher Zinszahlung.

Beispiel:
Anfangskapital (K0): 10000 €
Zinssatz pro Jahr (p): 6%
Zinsauszahlung: Quartalsweise, Zinsperioden im Jahr = 4
Anzahl der Quartale (v): 28
Gesucht: Endkapital (Kn)
Berechnung: 1 + 6 : (4 · 100) = 1,015
1,01528 = 1,517222 (Aufzinsungsfaktor)
1,51722 · 10000 € = 15172,22 €
Ermitteln der Anlagedauer
Wenn der Prozentsatz, das Anfangskapital bekannt ist und man berechnen möchte, wie lange man braucht, um auf ein gewünschtes Endkapital zu kommen, dann muss die Formel durch Logarithmus umgestellt werden, um die Anlagedauer (n), Quartale (v), Monate (m) oder Tage (t) zu ermitteln.