Arbeit und Energie

Wenn ein Körper bewegt wird, verrichtet man Arbeit. Somit resultiert Arbeit aus einem Produkt von Kraft und Weg. Dabei wird nur die Kraft berücksichtigt, die in Wegrichtung zeigt. Wenn man z.B. einen am Boden liegenden Körper in waagerechte Richtung zieht, dann braucht man hierfür zwar Energie, man verrichtet jedoch keine Arbeit.

Wenn man den Körper in die Höhe hebt, verrichtet man Arbeit, weil durch die Hebung Energie gespeichert wird. Ein Körper, in dem Energie gespeichert wird, kann wiederum Arbeit verrichten. Man könnte diesen z.B. über eine Seilrolle mit einem anderen Körper verbinden, den Körper nach unten stoßen und dadurch den anderen Körper heben. Dadurch kann man feststellen, dass Arbeit und Energie identisch sind. Deshalb benutzt man für beide Größen das Formelzeichen W.

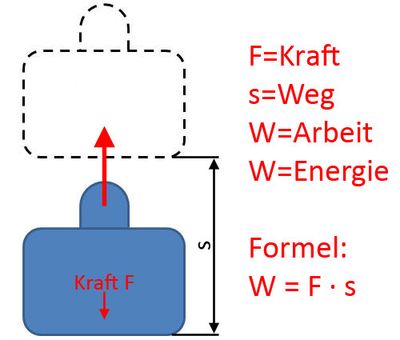
Die Formel ist W = F · s. Die Einheit wird in Joule angegeben, wobei 1 Newton · 1 Meter dem Wert von 1 Joule entspricht.

Bei den Formeln werden folgende Formelzeichen benutzt:

Arbeit: Formelzeichen W
Masse: Formelzeichen m
Fallbeschleunigung (Erdanziehungskraft 9,81 m/s²): Formelzeichen g
Kraft: Formelzeichen F
Gewichtskraft: Formelzeichen F_G, resultiert aus m · g, identisch mit Kraft
Weg: Formelzeichen s
Hubhöhe: Formelzeichen h, identisch mit Weg
Reibungszahl: Formelzeichen μ
Trägheitsmoment: Formelzeichen J
Geschwindigkeit: Formelzeichen v
Winkelgeschwindigkeit: Formelzeichen ω

Formel für Hubarbeit

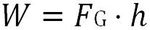
Bei der Hubarbeit wird durch eine Kraft ein Körper in die Höhe gehoben. Die Energie, die bei der Hubarbeit im Körper gespeichert wird, nennt man auch Lageenergie, Höhenenergie oder potenzielle Energie. Das Produkt aus Masse und der Erdanziehungskraft ergibt die Gewichtskraft F_G. Die Hubhöhe (h) ergibt den Weg.

Beispiel:

Masse des Körpers (m): 500 kg

Hubhöhe (h): 2 m

Gesucht: Gewichtskraft F_G und Hubarbeit W

Berechnung der Gewichtskraft: 500 · 9,81 = 4905 Newton

Berechnung der Hubarbeit: 4905 · 2 = 9810 Joule

Reibungsarbeit

Wenn ein Körper auf einer Unterlage bewegt wird, sodass die Reibung die Bewegung hemmt, wird Reibungsarbeit verrichtet. Genaugenommen wird auch bei der Hubarbeit Reibungsarbeit verrichtet, da in dem Fall die Reibung mit der Luft die Bewegung hemmt. Die Reibung mit der Luft ist jedoch so gering, dass diese bei der Hubarbeit nicht berücksichtigt wird. Anders als bei der Hubarbeit wird bei der Reibungsarbeit die Energie nicht gespeichert, sondern in Form von thermischer Energie (Wärme) an die Umgebung abgegeben.

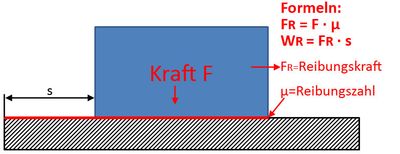
Eine wichtige Größe ist dabei die Reibungszahl. Damit wird angegeben, wie groß die Reibung zwischen zwei Körpern ist. Bei rollenden Körpern ist die Reibungszahl kleiner als bei nicht rollenden Körpern. Die Reibungskraft F_R ist die Kraft, die die Bewegung eines Körpers auf einem anderen Körper durch Reibung hemmt. Um den Körper zu bewegen, muss diese Hemmung überwunden werden. Bei einer Reibungszahl kleiner als 1 ist die Reibungskraft geringer als die Gewichtskraft. Daher muss man statt der vollen Gewichtskraft eine geringere Reibungskraft aufwenden, um den Körper zu bewegen. Die Formel für die Reibungskraft ist wie folgt:

F_R = F_G · μ

Da Arbeit aus Kraft mal Weg resultiert, berechnet man die Reibungsarbeit aus Reibungskraft mal Weg. Die Formel lautet daher:

W_R = F_R · s oder
W_R = F_G · μ · s

Beispiel:

Masse des Körpers (m): 500 kg

Weg (s): 2 m

Reibungszahl (μ): 0,4

Gesucht: Gewichtskraft F_G, Reibungskraft F_R und Reibungsarbeit W_R

Berechnung der Gewichtskraft: 500 · 9,81 = 4905 Newton

Berechnung der Reibungskraft: 4905 · 0,4 = 1962 Newton

Berechnung der Reibungsarbeit: 1962 · 2 = 3924 Joule

Spannenergie: Potenzielle Energie bei einer Feder

Wirkt eine Kraft auf eine Feder in Ruhelage, so dass man diese staucht oder streckt, wird potenzielle Energie gespeichert. Sie wird auch Spannenergie genannt, da hierbei die Feder gespannt wird. Um die Spannenergie berechnen zu können, braucht man zuerst die Federkonstante (D).

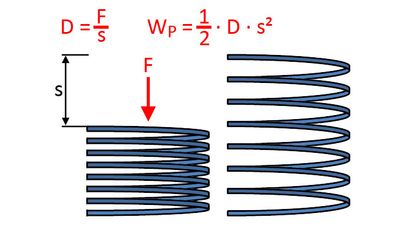
Die Formel hierfür ist:

D = F : s

Die Einheit für die Federkonstante ist Nm. Mit der Federkonstante und der folgenden Formel kann die Spannenergie berechnet werden:

W_P = 0,5 · D · s²

Beispiel:

Kraft (F): 4905 N

Weg (s): 4 m

Gesucht: Federkonstante D und die potenzielle Energie W_P

Berechnung der Federkonstante: 4905 : 4 = 1226,25 Nm

Berechnung der potenziellen Energie: 0,5 · 1226,25 · 16 = 9810 Joule

Kinetische Energie: Bewegungsenergie

Wird ein Körper aus der Ruheposition heraus in Bewegung gesetzt, erhält der Körper eine Bewegungsenergie, auch kinetische Energie genannt. Die Energie entspricht dabei der Arbeit, die man aufwenden muss, damit der Körper in Bewegung gesetzt werden kann. Die Bewegungsenergie ist abhängig von der Masse und Geschwindigkeit des Körpers.

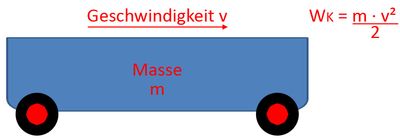
Die Formel ist:

W_K = m · v² : 2

Beispiel:

Masse (m): 2000 kg

Geschwindigkeit (v): 100 km/h = 27,77 m/s

Gesucht: Kinetische Energie W_K

Berechnung: 2000 · 771,60 : 2 = 771600 Joule = 771,6 KJ

Rotationsenergie: Kinetische Energie bei einer Drehbewegung

Wenn ein Körper aus der Ruheposition heraus um eine Rotationsachse in Bewegung gesetzt wird, erhält der Körper ebenfalls eine Bewegungsenergie. Diese Energie wird auch Rotationsenergie genannt. Sie ist abhängig vom Trägheitsmoment des Körpers und der Winkelgeschwindigkeit. Je weiter die Masse des Körpers von der Rotationsachse entfernt ist, umso mehr Arbeit ist nötig, um die Masse auf die Winkelgeschwindigkeit zu bringen.

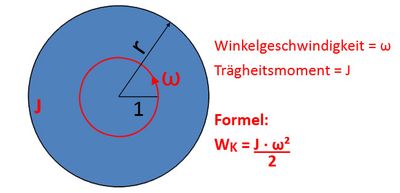
Die Formel für die Rotationsenergie ist:

W_K = J · ω² : 2

Beispiel:

Masse eines Vollzylinders (m): 500 kg

Radius des Vollzylinders (r): 0,25 m

Winkelgeschwindigkeit (ω): 15 s^-1

Gesucht: Trägheitsmoment J und Rotationsenergie W_K

Die Formel für den Trägheitsmoment beim Vollzylinder ist:

J = 0,5 · m · r²

Berechnung für J: 0,5 · 500 · 0,25² = 15,625 kgm²

Berechnung für W_K: 15,625 · 15² : 2 = 1757,8125 Joule